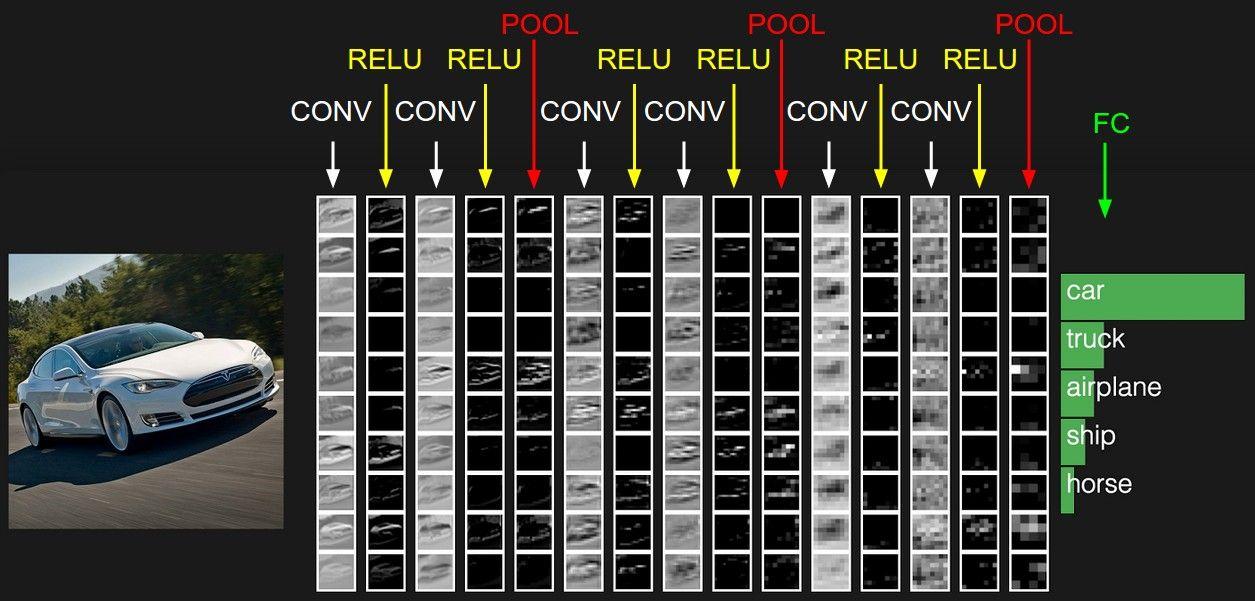
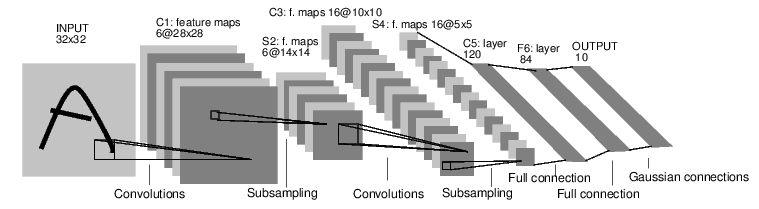
Convolutional Neural Network
Published:
Introduction
Convolutional Neural Networks or ConvNets or CNNs are biologically inspired varients of Multilayer Perceptrons(MLPs).They are probably the biggest reasons why AI agents are able to play ATARI games, are creating master piece artwork and cars have learnt to drive by themselves.Not only this, they are also being used in Natural language processing and text classification.
In this post, I will try to explain the basic architecture of the CNN.Much of the following content is derived from CS231n.It’s a great course and helps build the intuition of the working of CNN.Let me start by why is there a need for CNN and why it is becoming so popular.
Regular Neural Nets do not scale
Suppose we have a 200x200x3 size image(3 is the number of channels - R, G, B) and we input it to our first hidden layer in the regular neural nets.This would lead to a total of 200x200x3 = 120,000 weights.And that is just one layer.As we consider more number of layers, the parameters would add up quickly.Clearly, this full connectivity is wasteful and the huge number of parameters would quickly lead to overfitting.
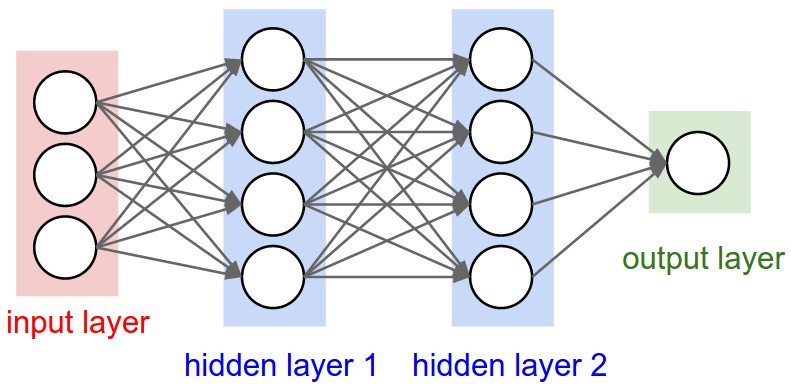
A regular 3-layer Neural Network
3D Volumes of Neurons
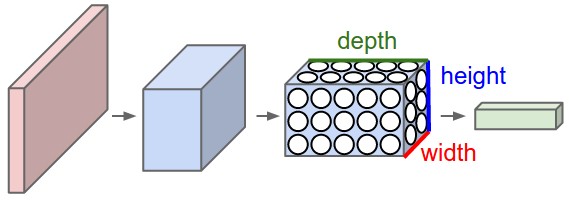
In particular, unlike a regular Neural Network, the layers of a ConvNet have neurons arranged in 3 dimensions: width, height, depth. (Note that the word depth here refers to the third dimension of an activation volume, not to the depth of a full Neural Network, which can refer to the total number of layers in a network.) For example, the input images in CIFAR-10 are an input volume of activations, and the volume has dimensions 32x32x3 (width, height, depth respectively). The neurons in a layer will only be connected to a small region of the layer before it, instead of all of the neurons in a fully-connected manner. This model is actually found in animal visual cortex.Individual cortical neurons respond to stimuli in a restricted region of space known as the receptive field. The receptive fields of different neurons partially overlap such that they tile the visual field. The response of an individual neuron to stimuli within its receptive field can be approximated mathematically by a convolution operation.
What is convolution?
Convolution can be thought of as a sliding window function applied to a matrix.This sliding window is called as filter, kernel or feature extractor.
CNN Architecture
Let’s take each component one by one.
Input layer
Unlike regular neural nets where we have one-dimensional input vector, here we have 3D image as the input.The three dimensions are height, width and channels (3 if RGB image, 1 if grayscale.)
Filter
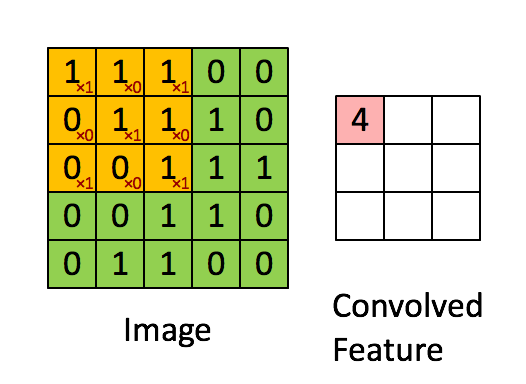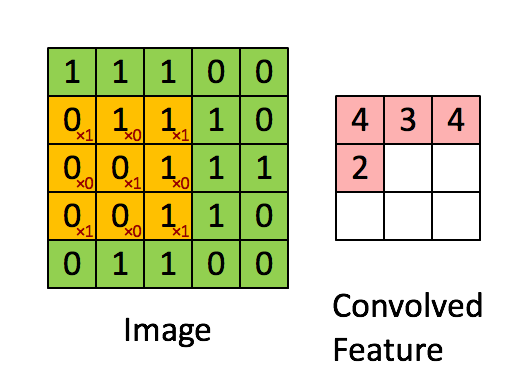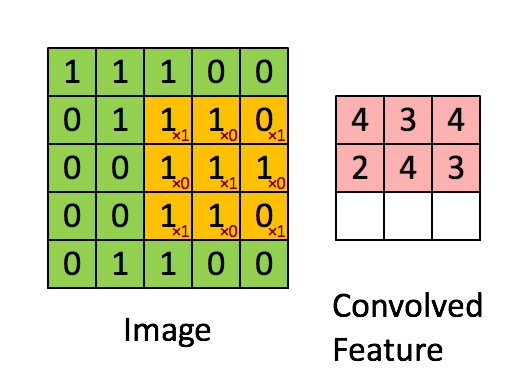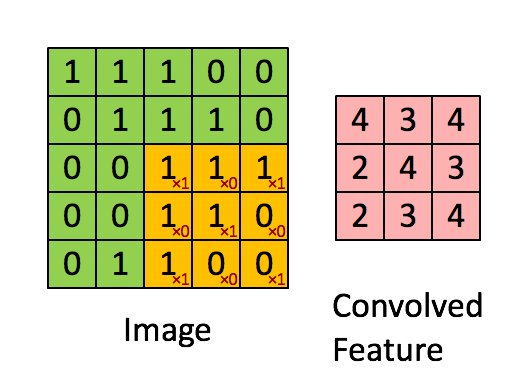
A filter is a matrix of weights which slides over the input image and does dot product with the image matrix just below it simultaneously.It then passes the result through a ReLU or tanH activation neuron thus outputting single element of activation map.The dimensions of a filter depend on the input thickness. If the input image/layer has 3 channels/thickness, the filter dimension would be something like 5x5x3.
Convolution layer
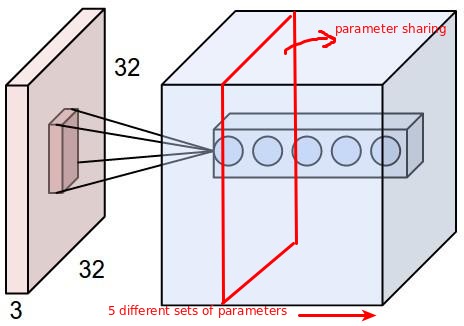
As we slide the filter over the input image, we get activations and all of them as a whole form one layer of activation map.The convolution layer is made up of these activation maps and each neuron on the activation map has a local connectivity with a local region in the input volume.Imagine flashing a torch on a flat transparent surface in a dark room with a condition that the light(yellow in color) doesn’t scatter as it penetrates the depth.The volume under this light would look like the part of the input volume that a convolution layer neuron is connected to at this particular moment.Sure, as we move our filter, the volume shifts accordingly but the dimensions and the weights remain the same. Let’s calculate the total number of weights connected to each neuron in each activation map.For a 5x5x3 filter, a input volume of 32x32x3 will produce 5x5x3 = 75 wights in one layer.
These weights are shared among all the other neurons in one activation map.If the output layer has 6 activation maps of dimension 28x28, then 75 weights will be shared by all the other 783 neurons on one activation map.This is called as parameter sharing.What about depth then?Are these weights also shared with each neuron accross the depth dimension.No, they are not.Infact there will be as many sets of weights as their are activation maps/filters.Imagine the torch light exampled I gave above.Now we have another torch that flashes a different color light say green.This torch would be just below the first one and covering the same area and volume.BUT, it’s a different color now.Similar is the case with activation maps in convolution layer.Each map has it’s own set of weights which are different than the maps above and below it but are shared among the neurons on the same map.The torch analogy might be a wrong example to state here but I hope this clears the picture a little.Following figure may make things clearer.
There is a simple math involved as to calculate the dimensions of output activation map depending on the the input and filter dimensions and quantity.
Output size = (N - F)/Stride + 1
where N = input spatial dimension (eg. a 32x32x3 image would have N = 32), F = filter dimension (eg. 3x3, 5x5, 11x11 )
The depth of the activation map or number of layers in the output(slices of activation maps) depend on the number of filters we are using.
Activation map depth = Number of filters used.
But what are strides ? Strides are the number of steps to move while sliding over input. There is one more thing left which is padding.Let’s look at the significance of padding by an example.Suppose we have a 32x32 image and we are using a filter of size 5x5.Taking stride as 1, what will be the dimension of the output after one convolution?
(N-F)/S + 1 = (32-5)/1 + 1 = 28
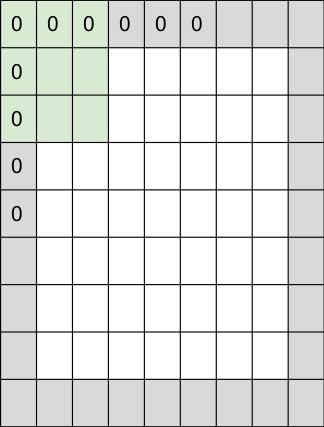
Okay, now let’s use this output as an input to out next convolution.The result will be 24. So we see that the output shrinks gradually at the beginning.This was just an example.In real life scenario, it shrinks even faster.Padding helps us avoid this situation by keeping the output dimension either same or more.It is a process in which the input is padded with 0's on height and width sides.For an example,in the following image, a 7x7 image has been padded with 1 pixel border.What is the corresponding output dimension?
N = 9, F = 3, S = 1
(N-F)/S + 1 = (9-3)/1 + 1 = 7
That’s same as the input! Thus we see that we can control the shrinking of our output by padding.We can also modify about formula to add padding.
(N−F+2P)/S + 1
where P is padding(0,1,2,3...)
Following formulae from CS231 summarize the convolution layer very well.
Input (W2xH2xD2) ---convolution--> Output (W2xH2xD2)
where W2 = (W1-F+2P)/S + 1
H2 = (H1-F+2P)/S + 1
D2 = K
Total number of weights per filter = FxFxD1
Total number of weights in a convolution layer = (FxFxD1)xK + K biases
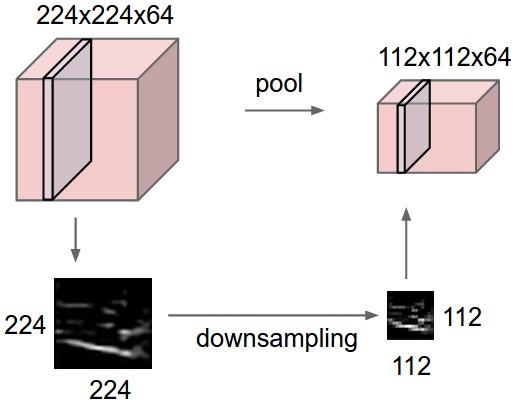
Pooling
Pooling let’s us control the spatial size of the output layer and thus controlling the number of parameters.It is usually inserted between two convolution layers.It is done one each activation map independently and preserves the depth dimension.In max pooling operation, a filter (eg. 2x2, stride 2) slides over one activation map and downsamples it to half of it’s previous dimensions.Following figure shows the max pooling operation.
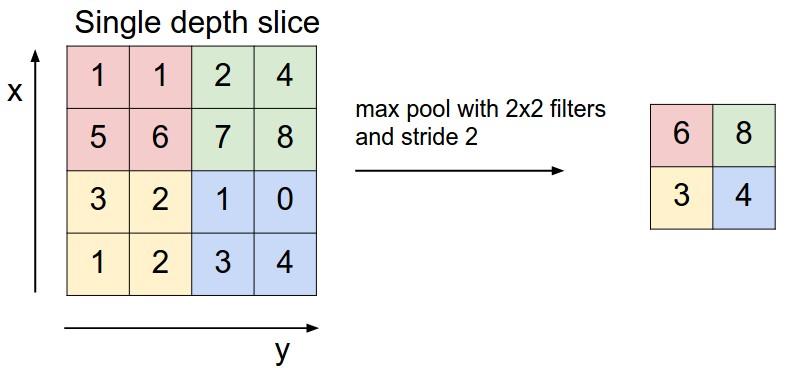
A very common max pooling operation done over a slice of activation map.Max operation is performed over 4 numbers at a time when a filter of 2x2 makes stride of 2
Fully connected layer
The neuron activations from the final convolution layers are flattened to produce a vector which acts as an input to a regular neural network called fully connected network.This network finally produces outputs like scores or probabilities associated with our original input volume.
Putting it all together
Though I have not covered all the details of a CNN network, above mentioned components are pretty much what is required for building a basic CNN network like handwritten digits classifier.In general, the full CNN architecture can be summarized by the following formula:
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC
where the * indicates repetition, and the POOL? indicates an optional pooling layer. Moreover, N >= 0 (and usually N <= 3 ), M >= 0 , K >= 0 (and usually K < 3 ).
I hope this post was useful in some way.Please follow for more interesting updates!